배열은 언제나 배열이었다
오늘은 자료구조에서 배열을 공부해보면서 좀더 색다른 매력을 느껴버렸다
자료구조 - Array(배열)이란
" 일정한 차례나 간격에 따라 벌여 놓음 " 이라는 뜻을 가지고 있다
차례(순서)에 관한 기본적인 자료 구조이다
인덱스 - 원소값 으로 구성 되어있다 (인덱스는 0번부터 시작하고 순서대로 값이 들어간다)
인덱스
배열의 원소들은 메모리 주소를 가지고 있고, 메모리 주소의 순서는 === 인덱스 순서와 일치한다
배열은 배열[인덱스] = 이런식으로 원소값에 직접 접근이 가능하다
배열과 인덱스로 알고리즘을 작성
↓
알고리즘에 따라 프로그램을 완성
↓
운영체제는 프로그램을 읽고 추상화된 언어를 해석해서 기계어로 번역해서 실행 (컴파일)
↓
사용자에게 제공
배열의 추상 자료형
배열의 정의와 연산을 알아보자
// 배열 생성
Array create(n) ::=
배열의 크기가 n인 빈배열을 생성, 반환
// 배열 원소값 찾기
Element retrieve(a, i) ::=
if(i ∈ index)
then { 배열의 i번째 원소값 e를 반환 }
else { 에러 메시지를 반환 }
// 배열 원소값 저장
Array store(a, i, e) ::=
if(i ∈ index)
then { a[i] = e 하고, a 를 반환 }
else { i > n 이면 에러 메시지 반환 }** Element 는 같은 원소형의 집합을 나타낸다
배열의 생성
매개변수로 받은 n 사이즈만큼
배열 a 를 선언하고, i 도 선언하고
for 문돌면서 a[i] 값을 0 으로 초기화해준다
void create(int n) [
int a[n]; // 배열 a를 선언
int i; // 인덱스 i를 선언
for(i = 0; i < n; i++){ // for문을 i만큼 돌리면서
a[i] = 0; // 초기값으로 0을 선언
}
}
배열의 검사
retrieve 함수는 원소 값을 찾아주는 함수이다.
일단 인덱스가 유효범위하에 있으면 원소값을 반환하고 그게 아니면 에러를 뱉어낸다.
#define array_size 5 // 배열 사이즈 정의
int retrieve(int *a, int i){ // 매개 변수로 배열 a 와 인덱스 i를 받는다
if(i >= 0 && i < array_size } { // i가 0이상 && 배열 사이즈보다 작을 때
return a[i]; // 해당 원소값을 반환!
} else {
printf('error'); // 예외 처리
return (-1);
}
}
배열의 저장
store 함수는 배열을 저장하기 위한 함수이다
매개변수로 배열 a랑 인덱스 그리고 저장할 값인 e를 받고,
인덱스가 유효범위 안에 있으면 a[i] = e; 로 단박에 저장해 버린다
#define array_size 5;
void store(int *a, int i, int e){ // 배열 a , 인덱스 i, 저장할 값 e
if(i >= 0 && i < array_size) { // i가 0 이상 && 배열 사이즈보다 작으면
a[i] = e; // a[i] 값으로 e 를 저 - 장
} else {
printf('error!') // 예외 처리
}
}
1차원 행렬
배열은 메모리를 할당받을 때 연속적으로 할당받는다 (추상적 순서 === 물리적 순서)
즉, 시작 주소만 알면 나머지 주소도 알 수 있다는 의미이다!
→ a[i] 의 저장주소는 시작주소 + (인덱스 * 비트수) 가 된다
→ a[i] 의 저장주소는 ⍺ + ( 𝑖 * 𝓴) 가 된다

2차원 행렬
이 친구도 배열이기 때문에 메모리를 연속적으로 할당받는다
다만 할당 순서를 행 먼저인지 열 먼저인지 정해주어야 한다 (컴파일러마다 다르다)
행우선 저장방식 & 열우선 저장방식
하나의 (행 | 열) 을 연속적으로 메모리에 할당하고,
그 다음 (행 | 열)을 메모리 영역에 할당하는 방식이다

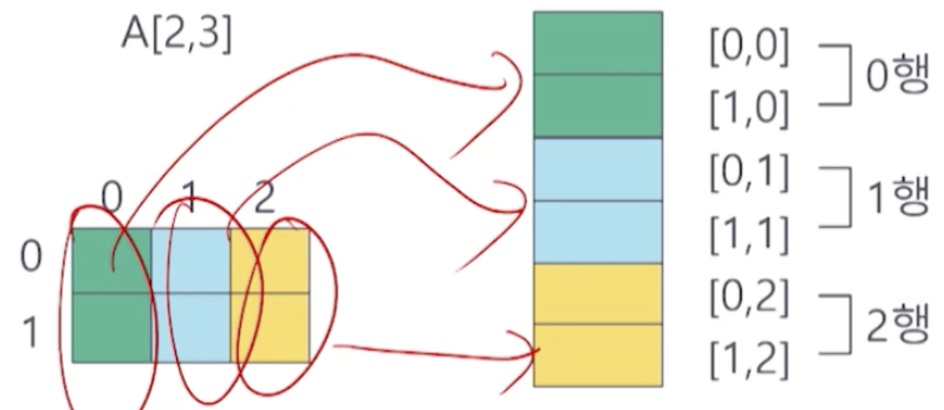
** 행우선 → 코볼, 파스칼, C / 열우선 → 포트란
희소 행렬
1차원 2차원 배열을 무사통과했으니 이젠 희소행렬이다
행열로 데이터를 나타낼 때 0이 겁나 많다면? 즉 빈값이 값보다 훨씬 많다면? (welcome to 희소행렬)
희소 행렬은 원소값이 0인 원소가 아닌 원소보다 상대적으로 많은 행렬이다
2차원 배열로 나타내면 아래와 같다 🤔🤔🤔

(메모리가 낭비되고 있다. 그렇기 때문에) 희소행렬은 조금 다르게 표현한다
기억에 남겨보려고 직접 테이블로 표를 짜보았다
→ 일단 0번째 인덱스는 total 데이터 (행 - 전체 행의 수 / 열 - 전체 열의 수 / 값 - 값이 있는 모든 원소의 갯수)
→ 예를 들어 행: 0 열: 1 에 해당하는 값은 20으로 표현
| i | 행 | 열 | 값 |
| 0 | 8 | 9 | 10 |
| 1 | 0 | 1 | 20 |
| 2 | 0 | 4 | 9 |
| 3 | 0 | 7 | 11 |
| 4 | 2 | 0 | 78 |
| 5 | 3 | 4 | 67 |
| 6 | 4 | 1 | 31 |
| 7 | 5 | 3 | 91 |
| 8 | 5 | 6 | 44 |
| 9 | 7 | 4 | 19 |
| 10 | 7 | 7 | 27 |
처음의 방대한(?) 2차원 배열과 비교해보면 희소행렬을 통해 알짜배기만 남았다 (72개 → 33개)
하지만 성능이 좋아지는 대신 연산이 복잡해진다 (득과 실을 따져서 효율적으로 사용하자)
'OS & Network' 카테고리의 다른 글
| 자료구조 - 연결리스트의 응용 (3) | 2023.12.01 |
|---|---|
| 자료구조 - 연결 리스트란 (1) | 2023.11.29 |
| 자료구조 - Queue(큐)란 (1) | 2023.11.24 |
| 자료구조 - Stack이란 (3) | 2023.11.23 |
| 안드로이드 - ADB 로 웹뷰 디버깅하기(WIFI 연결) (1) | 2023.10.11 |




댓글