1. 트리
트리는 논리적 계층을 가진 자료구조이고 트리의 종류는 다음과 같다
- binary tree
- heap
- binary search tree : AVL tree / BB tree / Splay tree
- m-way tree
- trie
- m-ary search tre : B-tree
2. 용어와 논리적 표현 방법
- 루트 : 트리에서 부모를 갖지 않은 노드
- 노드 : 트리를 구성하는 항목 aka 정점(vertex)
- 서브 트리: 루트 하위의 트리
- 진입 차수 : 노드로 들어오는 선의 개수
- 진출 차수 : 노드에서 나가는 선의 개수
- 내부 노드 : 루트도 잎도 아닌 노드
- 형제 : 같은 부모를 가진 노드
- 포화 이진 트리 : 이진 트리에서 각 레벨이 허용하는 최대 개수 노드를 가지는 트리
- 완전 이진 트리 : 높이가 k 인 이진 트리가 레벨 0 부터 k-2 까지 다 채우고, 마지막 k-1 레벨에서 왼쪽 → 오른쪽으로 채워진 트리
- 순회 : 트리의 각 노드를 빠짐없이 한 번씩만 방문하는 것
- 노드의 차수 : = 진출차수와 같다 ex) 자식으로 나가는 선의 개수 J = 2 / Sh = 1 ...
- 트리의 차수 : = 최대 노드의 차수 = 최대 진출 차수 ex) 최대는 2 !
- 노드의 레벨 : 루트로부터 노드까지 이어진 선의 갯수

중첩된 집합으로 표현

들여 쓰기로 표현

3. 추상 자료형
- 트리 객체의 정의 : 루트 노드를 갖는 유한 리스트
- 연산
TreeCreate() ::= 트리를 생성 + 루트노드 포인터를 반환
Destroy(Tree) ::= 더이상 사용하지x 트리의 메모리 할당 해제
TreeCopy(Tree) ::= 트리를 복사 + 복사한 트리의 루트 노드 포인터를 반환
Insert(n) ::= 노드 n을 삽입
Delete() ::= 노드 삭제 (재구성 단계를 포함)
Search() ::= 특정 키 값을 갖는 노드 검색 (찾으면 true, 아니면 false)
Traverse() ::= 트리를 순회, 방문 순서대로 값 반환
Root() ::= 루트 노드 값 반환
Parent(n) ::= n의 부모(data or pointer)를 반환, n이 루트면 오류!
Children() ::= n의 자식(data or pointer)를 반환, n이 루트면 오류!
IsRoot(n) ::= n이 루트이면 true 아님 false
IsLeaf(n) ::= n이 잎이면 true 아님 false
IsInternal(n) ::= n이 내부 노드면 true 아님 false
IsEmpty() ::= 트리가 비었으면 true 아님 false
Replace(n,m) ::= n을 m으로 변경
4. 이진 트리
모든 노드의 차수가 2 이하인 트리를 이진 트리라고 한다
이진트리는 수학적으로 이론을 정리하기 쉽고, 컴퓨터 내부에 구현도 쉽다
모든 노드가 2개 이하의 자식을 가지므로 오른쪽 왼쪽이라는 방향 개념도 부여 가능하다
- 포화 이진 트리
이진 트리의 각 레벨에서 최대 개수 노드를 가지는 트리
루트 레벨을 0 이라할 때, 높이가 k인 포화 이진트리의 노드갯수는 다음과 같다
(트리의 높이는 잎의 레벨에 1을 더한 것, 즉 아래 트리의 높이는 4가 된다)
2ª = 2ª - 1
예를 들어 높이가 3인 포화 이진 트리는 노드가 7개이고 높이가 4인 포화 이진트리는 노드가 1,023개 이다.
높이가 k인 이진 트리가 레벨 0부터 k-2까지 다 채우고 마지막 k-1 레벨에서 왼쪽부터 오른쪽으로 노드들이 차례로 채워졌을 때
완전 이진 트리라고 한다.
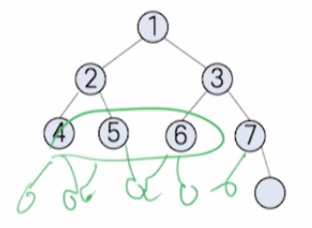
이진 트리는 연속된 배열에 저장할 수 있다.
이 방법은 이진 트리를 완전 이진 트리라 가정하고 각 레벨에 있는 노드를 대응하는 위치에 차례로 저장한다
이 방법은 트리가 포화 이진 트리 또는 완전 이진 트리인 경우 낭비되는 공간이 없어 효율적이다. 하지만 기억장소의 낭비가 2의 거듭제곱에 비례하며 심해진다는 것을 알 수 있다.
이러한 이유로 이진트리는 보통 연결리스트로 구현한다
이진 트리를 구현하기 위핸 연결리스트의 노드는 데이터, 왼쪽 서브트리 포인터, 오른쪽 서브트리 포인터로 구성한다.

5. 이진 트리 연산
- 이진 트리 순회
노드 구조체 정의
struct node {
struct node *left; // 왼쪽 포인터
struct node *right;// 오른쪽 포인터
int info; // 데이터
}
이진 트리의 순회 알고리즘
struct node *nodeptr;
// 전위 순회
void preorder(struct node *tree_ptr){
if(tree_ptr){
printf("%d", tree_ptr → info) // 루트를 먼저 방문(출력),
preorder(tree_ptr → left); // 왼쪽 서브트리 다돌고
preorder(tree_ptr → right);// 오른쪽 서브트리 순회
}
}
// 중위 순회
void inorder(struct node *tree_ptr){
if(tree_ptr){
inorder(tree_ptr → left); // 왼쪽 서브트리 중위 순회
printf("%d", tree_ptr → info); // 루트를 먼저 방문(출력),
inorder(tree_ptr → right); // 오른쪽 서브트리를 중위 순회
}
}
// 후위 순회
void postorder(struct node *tree_ptr){
if(tree_ptr){
postorder(tree_ptr → left); // 왼쪽 서브트리 후위순회
postorder(tree_ptr → right); // 오른쪽 서브트리 후위순회
printf("%d", tree_ptr → info); // 루트를 방문(출력)
}
}** 보통은 스택을 직접 운영하여 비순환으로 순회 함수 구현
- 이진 트리 생성, 삽입, 삭제
연결리스트 연산을 사용해 생성하면된다
- 먼저 노드 하나 생성 (루트가 될 몸)후,
- 이중연결리스트의 삽입 연산을 사용해 새로운 노드를 추가해서 구조를 만든다
삽입이나 삭제도 간단하다
- 삽입할 노드를 생성한 후 부모의 노드가 링크를 가리키게 하면 된다
- 삭제할 노드의 부모 노드의 링크를 null 로만들어서 끊어준다 (삭제할 노드가 잎일경우)
- 이진 트리 노드 개수 세기
int get_node_count (nodeptr *root) {
if(root == NULL) return 0;
int result = 1;
result +=
get_node_count(nodeptr*)root → left) + get_node_count(nodeptr*)root → right);
return result;
}
int get_leaf_count(nodeptr *root){
int result = 0;
if(root == NULL){
return 0;
} else if(root → left == NULL && root → right == NULL) {
return 1;
}
result +=
get_leaf_count((nodeptr*)root → left) + get_leaf_count((nodeptr*)root → right);
return result;
}
6. 일반 트리를 이진 트리로 변환
주어진 트리에 대해 각 노드의 형제들은 연결 합니다
다음으로 가장 왼족 링크만 남기고 모두 제거 합니다
다만 루트 노드는 반드시 왼쪽 자식 하나만 가지도록 합니다
(부모 노드는 왼쪽 / 형제노드 인경우 오른쪽)

7. 트리의 종류
- 합병 정렬 : 차례로 정렬한 데이터 리스트 k 개를 완전한 순서를 유지하는 하나의 리스트로 만드는 과정
- 선택 트리 : 합병 정렬에 사용하는 특수한 트리
- 승자 트리 : 각 노드(부모)가 < 두 자식 노드보다 더 작은값을 가지는 포화이진트리
- 패자 트리 : 각 노드가(부모) > 두 자식 노드보다 더 큰 값을 가지며 최종 승자는 0번 노드에 저장하는 트리
- 숲: 분리된 트리모임 n개 이상의 분리된 트리 집합
- 이진트리의 개수 : 노드 n 개인 서로다른 이진트리는 (2n)!/n!(n+1)!
'OS & Network' 카테고리의 다른 글
| Network - HTTP 살펴보기 (1) (Request / Response / Header) (1) | 2023.12.07 |
|---|---|
| 자료구조 - 스레드 트리 (1) | 2023.12.05 |
| 자료구조 - 연결리스트의 응용 (3) | 2023.12.01 |
| 자료구조 - 연결 리스트란 (1) | 2023.11.29 |
| 자료구조 - Array(배열)이란 (1) | 2023.11.26 |




댓글